| 图片 | ||
| 概念 | ||
| 问题 | ||
| README.md | ||
数学
数学,是研究数量、结构以及空间等概念及其变化的一门学科,从某种角度看属于形式科学的一种。数学利用抽象化和逻辑推理,从计数、计算、量度、对物体形状及运动的观察发展而成。数学家们拓展这些概念,以公式化新的猜想,以及从选定的公理及定义出发,严谨地推导出一些定理。
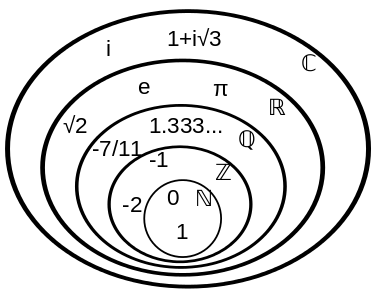
数
| 名称 | 符号 | 说明 |
|---|---|---|
| 阿拉伯数字 | 1\ 2\ 3\ 4\ 5\ 6\ 7\ 8\ 9\ 0 |
据说是古代印度人发明的 |
| 自然数 | \Bbb{N} |
\lbrace 0,1,2,3 \dots \rbrace |
| 正整数 | \Bbb{Z}^+ |
非零自然数 \lbrace 1,2,3,\dots \rbrace |
| 负整数 | \Bbb{Z}^- |
\lbrace \dots,-3,-2,-1 \rbrace |
| 整数 | \Bbb{Z} |
包括正整数、零和负整数 \lbrace \dots,-3,-2,-1,0,1,2,3,\dots \rbrace |
| 分数 | \dfrac{a}{b}\ \Big(a,b\in\Bbb{Z}且b\ne0\Big) |
a 称为分子, b 称为分母。用于表示有理数、比例、等分、整除、百分数,形式包括:最简分数、真分数、假分数、带分数 |
| 有理数 | \Bbb{Q} |
与分数是同义词,即可以写成分数的数 \Big\lbrace \dfrac{a}{b} \Big\| a,b\in\Bbb{Z} 且 b\ne0 \Big\rbrace |
| 实数 | \Bbb{R} |
包括有理数和无理数 |
| 小数 | 0.3,\ 0.\dot{3},\ \pi |
实数的一种特殊的表现形式,包括:有限小数、循环小数、无限不循环小数 |
算
四则运算,即加减乘除($+-\times\div$),是数学最基本的算术运算。在同一个算式列中,其运算次序是“括号内先算,先乘除,后加减”。
加法将数个数(称为加数)组合起来得到总量(称为和)。将多个一相加称为计数。一个数加零仍等于自身。加法拥有交换律 \boxed{a+b=b+a} 和结合律 \boxed{(a+b)+c=a+(b+c)} ,即多个加数的顺序可以任意调换,而和不变。十进制多位数加法的标准计算方式是竖式计算,即各位竖向对齐,从个位开始逐位相加,超过9的部分进位到更高位。
加法竖式计算:
$\begin{array}{cccc} &1 &2 &9 \ + & &_1 &6 \ \hline = &1 &3 &5 \end{array}$
减法指从被减数中移除减数,结果称作差。减法可视为“加法的逆运算”,即当 x+y=z 时 z-y=x 且 z-x=y 。减去一个数等于加上这个数的相反数,例如: 6-3=3=6+(-3) 。若果被减数小于减数,得出来的差将会是负数,例如: 3-6=-3 。
减法竖式计算:
$\begin{array}{cccc} &3^. &1 &4 \ - &1 &4 &1 \ \hline = &1 &7 &3 \end{array}$
乘法是加法的连续运算,同一数(被乘数)的若干次(乘数)连加,其运算结果称为积,例如:
\sum_{k=1}^{n}a = \underbrace{a + a + a + \cdots + a}_{n} = a \times n 写作 $a \times n$,也可写作 a \cdot n 或 an ,读作a乘以n,或n乘a。
乘法口诀表
\times |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 10 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 100 | 110 | 120 |
| 11 | 11 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 110 | 121 | 132 |
| 12 | 12 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 120 | 132 | 144 |
乘法竖式计算:
$\begin{array}{cccc} & &1 &8 \ \times & &2 &3 \ \hline & &5 &4 \ + &3 &6 \ \hline = &4 &1 &4 \end{array}$
任何数乘以零,结果是零,即 0x=0 。
任何数乘以一都等于该数本身,即 1x=x ,称为单位律。
当 x 是量, y 是自然数,乘法的递归定义为:
\begin{dcases} 0x=x \\ xy=x+x(y-1) \end{dcases}
乘法拥有交换律 $\boxed{a \times b = b \times a}$,结合律 \boxed{(a \times b) \times c = a \times (b \times c)} 和 分配律 \boxed{a \times (b+c)= a\times b + a\times c}
除法可以看成是“乘法的反运算”,也可以理解为“重复的减法”。如果 a \times b = c 且 b \ne 0 则 $a = c \div b$,其中 a 称商数, c 称被除数, b 称除数。
如果除式的商数 a 必须为整数,则称为带余除法, c - a \times b 的值称为余数( d ),写作: $c \div b = a \dots d$,读作:c除以b等于a余d。当 d=0 时称 b 整除 $c$,写作 b \big| c ,即 c 是 b 的倍数, b 是 c 的因数或约数。
计算大数除法使用长除法(直式除法)
判断能否被整数n整除
- 2:个位是偶数
- 3:各位数之和是3的倍数
- 4:末两位数是4的倍数
- 5:个位为0和5
- 6:各位数之和是3的倍数的偶数
- 7:截去个位后减去个位数的2倍的差是7的倍数(可重复操作)
- 8:百位以内的数是8的倍数
- 9:各位数之和是9的倍数
- 10:个位是0
- 11:截去个位后减去个位数的差是11的倍数(可重复操作); 各奇数位之和和各偶数位之和的差是11的倍数;
- 12:同时是3和4的倍数
- 13:截尾、4倍大、相加、验和
- 14:7的偶数倍
- 15:同时是3和5的倍数
比、比例、比值、正比例、反比例
质数、合数、分解(质)因数、互质
分数运算:分数的加减法、通分、约分、分数的乘除法
小数运算:小数点对齐再运算,结果中小数点位置的确定
巧算公式
\dfrac{1}{n \times (n+1)} = \dfrac{1}{n} - \dfrac{1}{n+1}\dfrac{d}{n \times (n+d)} = \dfrac{1}{n} - \dfrac{1}{n+d}\dfrac{1}{n \times (n+d)} = \dfrac{1}{d} \times (\dfrac{1}{n} - \dfrac{1}{n+d})
量(单位)
国际单位制以七个基本单位为基础,由此建立起一系列相互换算关系明确的“一致单位”。
做题时必须将单位统一!!!
- 长度:毫米$mm$、厘米$cm$、分米$dm$、米$m$、千米
km- 换算:
1000毫米=100厘米=10分米=1米=0.001千米
- 换算:
- 面积:平方厘米$cm^2$、平方米$m^2$、亩、公顷
hm^2- 换算:
1亩=666.\dot6平方米,1公顷=15亩=10000平方米, 1平方千米=100公顷
- 换算:
- 体积:立方厘米$cm^3$、立方米
m^3- 换算:
1立方米=1\times10^6立方厘米
- 换算:
- 容积:毫升$ml$、升
l- 换算:
1升=1000毫升
- 换算:
- 质量:克$g$、千克$kg$、吨$t$、斤
- 换算:
1吨=1000千克=2000斤=1\times10^6克 - 常见:一个鸡蛋约50克
- 换算:
- 价格:元角分
- 时间:年月日时分秒
- 角度:度、弧度
形
点:顶点、垂点、圆心
线:直线、线段、射线、边、对角线
角:角度、零角、锐角、直角、钝角、平角、周角、内角、外角
\angle 0^\circ 零角 \lt 锐角 \lt \angle 90^\circ 直角 \lt 钝角 \lt \angle 180^\circ 平角 \lt \angle360^\circ 周角 量取角度的要点:
1. 中心对准顶点
2. 0度对准一边
3. 仔细读取角度
形:轴对称、中心对称、多边形、多边形内角和、周长、面积
平移、旋转
- 多边形:
- 三角形
- 锐角三角形
- 直角三角形
- 钝角三角形
- 等边三角形
- 等腰三角形
- 四边形
- 平行四边形
- 矩形
- 长方形
- 正方形
- 斜方形
- 菱形
- 矩形
- 梯形
- 筝形
- 平行四边形
- 三角形
- 圆
体
正面、侧面、顶面
长方体、正方体、圆柱体、圆锥、球体
方程
含有未知数的等式
公式
| 名称 | 公式(周长C,(表)面积A,体积V) | 说明 |
|---|---|---|
| 三角形 | A=\dfrac{1}{2}(底\times高) |
|
| 三角形 | A=\dfrac{1}{2}ab\cdot\sin\theta |
$a, b, \theta$为已知的两边及其夹角 |
| 三角形 | A=\sqrt{s(s-a)(s-b)(s-c)} |
海龙公式,$s$为三角形半周长 |
| 三角形 | A=sr |
$s$为三角形半周长,$r$为三角形内切圆半径 |
| 三角形 | A=\dfrac{abc}{4R} |
$R$为三角形外接圆半径 |
| 四边形 | A=\dfrac{1}{2}pq\cdot\sin\theta |
$p, q, \theta$为对角线长度及其夹角 |
| 菱形 筝形 | A=\dfrac{1}{2}pq |
$p, q$为对角线长度 |
| 平行四边形 | A=底\times高 |
|
| 长方形 | A=长\times宽 |
|
| 正方形 | A=边长^2 |
|
| 梯形 | A=\dfrac{1}{2}(上底+下底)\times高 |
|
| 圆 | C=2 \pi r |
|
| 圆 | A=\pi r^2 |
|
| 长方体 | A=2(ab+bc+ac) |
|
| 长方体 | V=abc |
|
| 正方体 | A=6a^2 |
|
| 正方体 | V=a^3 |
|
| 圆柱体 | A=4 \pi r^2 + 2 \pi rh |
|
| 圆柱体 | V=\pi r^2 \cdot h |
|
| 圆锥体 | A=\pi r^2+\pi rl |
|
| 圆锥体 | V=\dfrac{1}{3} \pi r^2 \cdot h |
|
| 球体 | A=4 \pi r^2 |
|
| 球体 | V=\frac{4}{3} \pi r^3 |
|
统计
- 统计表
- 统计图
- 可能性:随机事件所有可能中的一部分占总数的比例。
- 方向:上北下南,左西右东。北偏东$30\degree$(时钟1点钟方向)。
\begin{array}{ccccc}
&西北 & &北 & &东北 \\
& &\nwarrow &\uparrow &\nearrow & \\
&西 &\leftarrow &中 &\rightarrow &东 \\
& &\swarrow &\downarrow &\searrow & \\
&西南 & &南 & &东南
\end{array}$$
<script type="text/javascript" src="http://cdn.mathjax.org/mathjax/latest/MathJax.js?config=TeX-AMS-MML_HTMLorMML"></script>
<script type="text/x-mathjax-config"> MathJax.Hub.Config({ tex2jax: {inlineMath: [['$', '$']]}, messageStyle: "none" });</script>